![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics & Computer Science |
 |
Next: Completion procedure
Up: Rewriting for Kan Extensions
Previous: Rewriting for Kan Extensions
To work with a rewrite system 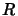 on
on 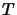 we will require certain
concepts of order on
we will require certain
concepts of order on 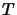 . We give properties of orderings
. We give properties of orderings 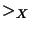 on
on
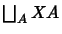 and
and 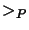 on
on
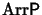 to enable us to
construct an ordering
to enable us to
construct an ordering 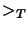 on
on 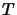 with the properties needed for
the rewriting procedures.
Given an admissible well-ordering
with the properties needed for
the rewriting procedures.
Given an admissible well-ordering 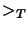 on
on 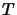 it is
possible to discuss when a reduction relation generated by a
rewrite system is compatible with this ordering.
It is a standard result that if a reduction relation is compatible
with an admissible well-ordering, then it is Noetherian.
A Noetherian reduction relation on a set is confluent if it is
locally confluent
(Newman's Lemma
[16]).
By standard abuse of
notation the rewrite system
it is
possible to discuss when a reduction relation generated by a
rewrite system is compatible with this ordering.
It is a standard result that if a reduction relation is compatible
with an admissible well-ordering, then it is Noetherian.
A Noetherian reduction relation on a set is confluent if it is
locally confluent
(Newman's Lemma
[16]).
By standard abuse of
notation the rewrite system 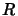 will be called complete when
will be called complete when 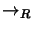 is
complete.
Hence, if
is
complete.
Hence, if 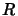 is compatible with an admissible well-ordering on
is compatible with an admissible well-ordering on
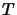 and
and 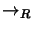 is locally confluent then
is locally confluent then 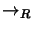 is complete. By
orienting the pairs of
is complete. By
orienting the pairs of 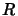 with respect to the chosen ordering
with respect to the chosen ordering
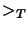 on
on 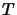 ,
, 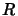 is made to be Noetherian. The problem remaining
is testing for local confluence of
is made to be Noetherian. The problem remaining
is testing for local confluence of 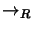 and changing
and changing 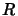 in
order to obtain an equivalent confluent reduction relation.
We explain the notion of critical pair for a rewrite
system for
in
order to obtain an equivalent confluent reduction relation.
We explain the notion of critical pair for a rewrite
system for 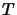 , extending the traditional notion to our situation.
In particular the overlaps involve either just
, extending the traditional notion to our situation.
In particular the overlaps involve either just 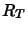 , or just
, or just
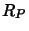 or an interaction between
or an interaction between 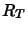 and
and 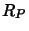 .
.
A term 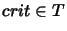 is called critical if it may be reduced by
two or more different rules.
A pair
is called critical if it may be reduced by
two or more different rules.
A pair
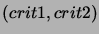 of distinct terms resulting from two single-step
reductions of the same term is called a critical pair.
A critical pair for a reduction relation
of distinct terms resulting from two single-step
reductions of the same term is called a critical pair.
A critical pair for a reduction relation 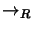 is said to
resolve if
there exists a term
is said to
resolve if
there exists a term 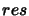 such that both
such that both 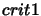 and
and 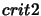 reduce to a
reduce to a
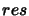 , i.e.
, i.e.
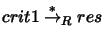 ,
,
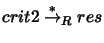 .
If
.
If
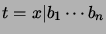 , then a part of
, then a part of 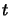 is either a term
is either a term
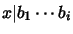 for some
for some
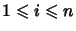 or a word
or a word
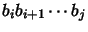 for some
for some
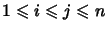 .
Let
.
Let
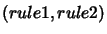 be a pair of rules of the rewrite
system
be a pair of rules of the rewrite
system
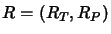 where
where
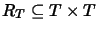 and
and
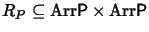 . Then the rules are said to overlap
when
. Then the rules are said to overlap
when 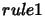 and
and 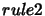 may both be applied to the same term
may both be applied to the same term 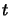 in such a way
that there is a part
in such a way
that there is a part 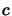 of the term that is affected by both the rules.
There are five types of overlap for this kind of rewrite system,
as shown in the following table:
of the term that is affected by both the rules.
There are five types of overlap for this kind of rewrite system,
as shown in the following table:
Next: Completion procedure
Up: Rewriting for Kan Extensions
Previous: Rewriting for Kan Extensions
Author: A. Heyworth, tel: +44 (0)116 252 3884
Last updated: 2000-11-24
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![]() is called critical if it may be reduced by
two or more different rules.
A pair
is called critical if it may be reduced by
two or more different rules.
A pair
![]() of distinct terms resulting from two single-step
reductions of the same term is called a critical pair.
A critical pair for a reduction relation
of distinct terms resulting from two single-step
reductions of the same term is called a critical pair.
A critical pair for a reduction relation ![]() is said to
resolve if
there exists a term
is said to
resolve if
there exists a term ![]() such that both
such that both ![]() and
and ![]() reduce to a
reduce to a
![]() , i.e.
, i.e.
![]() ,
,
![]() .
If
.
If
![]() , then a part of
, then a part of ![]() is either a term
is either a term
![]() for some
for some
![]() or a word
or a word
![]() for some
for some
![]() .
Let
.
Let
![]() be a pair of rules of the rewrite
system
be a pair of rules of the rewrite
system
![]() where
where
![]() and
and
![]() . Then the rules are said to overlap
when
. Then the rules are said to overlap
when ![]() and
and ![]() may both be applied to the same term
may both be applied to the same term ![]() in such a way
that there is a part
in such a way
that there is a part ![]() of the term that is affected by both the rules.
There are five types of overlap for this kind of rewrite system,
as shown in the following table:
of the term that is affected by both the rules.
There are five types of overlap for this kind of rewrite system,
as shown in the following table: