Tree-Resolution complexity of the Weak Pigeon-Hole Principle1

Stefan Dantchev²
Dept. of Mathematics and Computer Science, University of Leicester
dantchev@mcs.le.ac.uk
Søren Riis
Dept. of Computer Science, Queen Mary, University of London
smriis@dcs.qmw.ac.uk

Abstract:

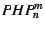
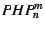
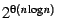
We show some tight results about the tree-resolution complexity of the Weak Pigeon-Hole Principle, $PHP_{n}^{m}$ . We prove that any optimal tree-resolution proof of $PHP_{n}^{m}$ is of size $2^{\theta \left(n\log n\right)}$ , independently from

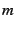
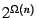
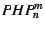
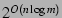
, even if it is infinity. So far, the lower bound know has been $2^{\Omega \left(n\right)}$ . We also show that any, not necessarily optimal, regular tree-resolution proof $PHP_{n}^{m}$ is bounded by $2^{O\left(n\log m\right)}$ . To best of our knowledge, this is the first time, worst-case proofs have been considered, and a non-trivial upper bound has been proven. 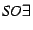Finally, we discuss and conjecture some refinements of Riis' Complexity Gap theorem for tree-resolution complexity of Second Order Existential ( $SO\exists$ ) sentences of predicate logic.

Keywords Propositional Proof Complexity, Tree-Resolution, Weak Pigeon-Hole Principle