![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif) | Department of Mathematics & Computer Science |
 |
Next: Applications
Up: paper10
Previous: Completion procedure
Example of a GAP Session on the Rewriting Procedure
Here we give an example to show the use of the implementation.
Let
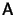 and
and
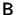 be the categories generated by the graphs
below, where
be the categories generated by the graphs
below, where
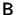 has the relation
has the relation
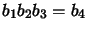 .
.
Let
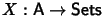 be defined by
with
be defined by
with
,
and let
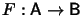 be defined by
and
. The input to the computer program
takes the following form.
First read in the program and set up the variables:
be defined by
and
. The input to the computer program
takes the following form.
First read in the program and set up the variables:
gap> RequirePackage("kan");
gap> F:=FreeGroup("b1","b2","b3","b4","b5","x1","x2","x3","y1","y2");;
gap> b1:=F.1;;b2:=F.2;;b3:=F.3;;b4:=F.4;;b5:=F.5;;
gap> x1:=F.6;;x2:=F.7;;x3:=F.8;;y1:=F.9;;y2:=F.10;;
Then we input the data (choice of names is unimportant):
gap> OBJa:=[1,2];;
gap> ARRa:=[[1,2],[2,1]];;
gap> OBJb:=[1,2,3];;
gap> ARRb:=[[b1,1,2],[b2,2,3],[b3,3,1],[b4,1,1],[b5,1,3]];;
gap> RELb:=[[b1*b2*b3,b4]];;
gap> fOBa:=[1,2];;
gap> fARRa:=[b1,b2*b3];;
gap> xOBa:=[[x1,x2,x3],[y1,y2]];;
gap> xARRa:=[[y1,y2,y1],[x1,x2]];;
To combine all this data in one record (the field names are important):
gap> KAN:=rec( ObA:=OBJa, ArrA:=ARRa, ObB:=OBJb, ArrB:=ARRb, RelB:=RELb,
FObA:=fOBa, FArrA:=fARRa, XObA:=xOBa, XArrA:=xARRa );;
To calculate the initial rules do:
gap> InitialRules( KAN );
The output will be:
i= 1, XA= [ x1, x2, x3 ], Ax= x1, rule= [ x1*b1, y1 ]
i= 1, XA= [ x1, x2, x3 ], Ax= x2, rule= [ x2*b1, y2 ]
i= 1, XA= [ x1, x2, x3 ], Ax= x3, rule= [ x3*b1, y1 ]
i= 2, XA= [ y1, y2 ], Ax= y1, rule= [ y1*b2*b3, x1 ]
i= 2, XA= [ y1, y2 ], Ax= y2, rule= [ y2*b2*b3, x2 ]
[ [ b1*b2*b3, b4 ], [ x1*b1, y1 ], [ x2*b1, y2 ], [ x3*b1, y1 ],
[ y1*b2*b3, x1 ], [ y2*b2*b3, x2 ] ]
This means that there are five initial
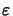 -rules:
-rules:
i.e.
and one initial 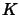 -rule:
.
To attempt to complete the Kan extension presentation do:
-rule:
.
To attempt to complete the Kan extension presentation do:
gap> KB( InitialRules(KAN) );
The output is:
[ [ x1*b1, y1 ], [ x1*b4, x1 ], [ x2*b1, y2 ], [ x2*b4, x2 ], [ x3*b1, y1 ],
[ x3*b4, x1 ], [ b1*b2*b3, b4 ], [ y1*b2*b3, x1 ], [ y2*b2*b3, x2 ] ]
In other words to complete the system we have to add the rules
and
The result of attempting to compute the sets by doing:
gap> Kan(KAN);
is a long list and then:
enumeration limit exceeded: complete rewrite system is:
[ [ x1*b1, y1 ], [ x1*b4, x1 ], [ x2*b1, y2 ], [ x2*b4, x2 ], [ x3*b1, y1 ],
[ x3*b4, x1 ], [ b1*b2*b3, b4 ], [ y1*b2*b3, x1 ], [ y2*b2*b3, x2 ] ]
This means that the sets 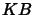 for
for 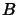 in
in
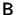 are too large. The
limit set in the program is 1000. (To change this the user should type
EnumerationLimit:= 5000 - or whatever, after reading in the program.)
In fact the above example is
infinite.
The complete rewrite system is output instead of the
sets. We can in fact use this to obtain regular expressions for
the sets. In this case the regular expressions are:
The actions of the arrows are defined by concatenation followed by
reduction.
are too large. The
limit set in the program is 1000. (To change this the user should type
EnumerationLimit:= 5000 - or whatever, after reading in the program.)
In fact the above example is
infinite.
The complete rewrite system is output instead of the
sets. We can in fact use this to obtain regular expressions for
the sets. In this case the regular expressions are:
The actions of the arrows are defined by concatenation followed by
reduction.
For example
is an element of
, so acts on it to give
which
is irreducible, and an element of .
The general method of obtaining regular expressions for these
computations will be given in a separate paper (see Chapter 4 of
[8]).
Next: Applications
Up: paper10
Previous: Completion procedure
Author: A. Heyworth, tel: +44 (0)116 252 3884
Last updated: 2000-11-24
MCS Web Maintainer
This document has been approved by the Head of Department.
© University of Leicester.
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)
![[The University of Leicester]](http://www.le.ac.uk/corporateid/departmentresource/000066/unilogo.gif)