We prove exponential lower bounds on the resolution proofs of some tautologies,
based on rectangular grid graphs. More specifically, we show a
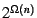
lower bound for any
resolution proof of
the mutilated chessboard
problem on a
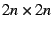
chessboard as well as for
the Tseitin tautology based on the
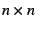 rectangular grid graph
rectangular grid graph. The former result answers a 35 year old
conjecture by McCarthy.